5 minutes pour comprendre les intérêts composés
Plus que 5 minutes pour comprendre les intérêts composés ! Enfin, j’espère ! Je vais essayer de vous expliquer comment, grâce à eux, vous allez vous mettre à l’abri financièrement parlant.
Les intérêts composés c’est cette petite formule qui a permis de bâtir des fortunes tout au long de l’histoire. C’est aussi le fameux « l’argent appelle l’argent ».
Description des intérêts composés
Imaginez que vous placiez 10 000 euros à 10%.
Au bout d’un an vous aurez dans votre escarcelle 11 000 euros (10 000 + 10 000 x 10/100, ou encore 10 000 x (1 + 10/100)).
Pour l’année d’après, 11 000 x (1 + 10/100) = 12 100 euros
Etc…
Au bout de n années, le capital se monte à
K x puissance(1 + i ; n)
où :
- i est le taux d’intérêt (0,1 pour 10%)
- K est le capital de départ
Utiliser un tableur pour les calculer
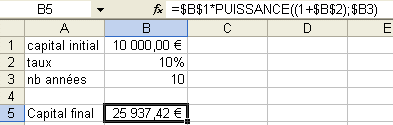
Il est facile de calculer le capital atteint au bout d’un nombre d’années avec un montant placé à un taux donné. Voici la formule :
Vous voyez, ce n’est pas compliqué.
Une règle sympathique :
pour doubler son capital il faut que taux et nombre d’années vérifient :
i x n = 70
Par exemple, pour doubler son capital à 20% il faut 3,5 années.
Pour doubler son capital à 2% il faut 35 ans.
Quelques résultats
Le tableau suivant montre quelques résultats pour un capital de départ de 10 000 euros, un taux variant de 1 à 30% et un nombre d’années variant de 10 à 20 ans.
| Taux | 10 ans | 15 ans | 20 ans |
|---|---|---|---|
| 1% | 11 046 | 11 609 | 12 201 |
| 2% | 12 189 | 13 458 | 14 859 |
| 5% | 16 288 | 20 789 | 26 532 |
| 7% | 19 671 | 27 590 | 38 696 |
| 10% | 25 937 | 41 772 | 67 274 |
| 20% | 61 917 | 154 070 | 383 375 |
| 30% | 137 858 | 511 858 | 1 900 496 |
Il est clair que placer son argent sur un livret bancaire (à 1% grosso-modo) c’est quasiment inutile.
Autre conclusion : il faut investir très tôt dans la vie, car plus les années passent, plus on gagne.
D’autre part, je vous entends déjà dire « mais comment faire du 10% par an ? Encore moins du 30% ! Nous allons aborder ce point un peu plus loin. J’aimerais d’abord vous entretenir de deux problèmes particuliers.
L’impact de l’inflation et des taxes
L’inflation et les taux d’intérêts composés
Vous n’êtes pas sans savoir qu’il existe un phénomène appelé l’inflation qui fait que le prix de l’excellent Mickey-Parade à sextuplé depuis 1985 (environ 5 Francs en 1985, aujourd’hui plus de 4,5 euros). L’argent d’aujourd’hui ne vaut plus rien par rapport à celui de cette année-là.
L’argent fond comme neige au soleil, et à un taux plus élevé que le très officiel taux de 1%.
Si vous placez votre capital sur un livret bancaire à, soyons grand prince, 1,75%, avec une inflation à 3%, il vous suffit de remplacer dans la formule 1,75 par 1,75 – 3 = -1,25.
Cela donne : 8 818 euros en 10 ans, soit une perte de 1 181 euros ! On n’épargne donc pas, on donne notre argent à la banque.
Les impôts et les taux d’intérêts composés
À l’inflation s’ajoutent les impôts. Supposons que le taux d’imposition soit de 25% des gains, au lieu de gagner 1% vous allez gagner 0,75%, au lieu de gagner 10%, vous allez gagner 7,5%…
On le voit, pour vraiment gagner de l’argent il faut un taux d’intérêt supérieur à 5% pour ouvrir les taxes et l’inflation.
Mais alors, je vous entends déjà me demander où trouver de tels taux ? 5% passe encore, mais 10% ?
Où trouver de forts taux d’intérêts ?
Vous trouverez de forts taux d’intérêts :
- dans l’immobilier, en louant des meublés en saisonnier (mais cela demande du travail) (voir « Comment calculer le rendement de son investissement locatif »)
- en bourse ou sur le Forex (voir « Technique pour gagner 1 million sans apport initial » et « Vous aussi gagnez bientôt votre salaire sans rien faire »)
- en faisant du business, en montant votre boîte (là aussi cela demande beaucoup de travail)
Vous pouvez bien sûr panacher les 3 voies : « Stratégies pour devenir riche même quand on est salarié »
Dans un prochain article nous apprendrons comment calculer le taux de rendement interne d’un projet. À bientôt.
Crédits image :